日程安排:

报告题目及摘要
Some new results and methods in bifurcation theory and their applications
代国伟
大连理工大学
This talk contains three parts. In the first part, we introduce the history of bifurcation theory and present some new global bifurcation theorems of nonlinear operator equations. In the second part, we mainly introduce the method of branches approximating and interval bifurcation. In the last part, we give several applications of the above theory and methods.
Semilinear elliptic equations with critical growth and Hardy potential
韩丕功
中国科学院
Semilinear elliptic equations arise from many mathematical models in physics, chemistry and biology or other branches of mathematics (such as Yamabe problem and isoperimetric inequality in geometry, Hardy Littlewood Sobolev inequality in Harmonic analysis). In this talk, I will introduce a series of results on the existence, multiplicity and singularity of solutions to elliptic equations with critical growth and Hardy potential.
Hardy-Littlewood-Sobolev inequality on compact manifold with boundary
韩亚洲
中国计量大学
In this talk, we establish the Hardy-Littlewood-Sobolev (HLS) inequality on smooth compact Riemannian manifold  with boundary. By localization, we prove that the sharp
with boundary. By localization, we prove that the sharp
constant  is greater than
is greater than , which is the sharp constant of HLS inequality on the upper half space
, which is the sharp constant of HLS inequality on the upper half space  ,which is the sharp constant of HLS inequality on the upper half space
,which is the sharp constant of HLS inequality on the upper half space  and it is equal to
and it is equal to 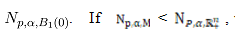 we employ the concentration-compactness principle to show existence of the extremal functions. While for the HLS on
we employ the concentration-compactness principle to show existence of the extremal functions. While for the HLS on  to overcome the difficult brought from the blowup, we adapt a class of renormalization method to construct the extremal function.
to overcome the difficult brought from the blowup, we adapt a class of renormalization method to construct the extremal function.
Some results on doubly coupled nonlinear Schrödinger systems
田如顺
首都师范大学
In this talk, we present some results on the following elliptic system,
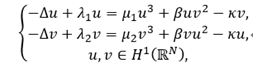
whereλ_j,β,κare constants. By using variational methods and bifurcation theory, we obtain some results on the positive solutions of this system.
From Allen-Cahn equation to Toda system and back
王克磊
武汉大学
In this talk I will discuss the derivation of Toda system from Allen-Cahn equation, and its application to some problems on Allen-Cahn equation such as the second order regularity of level sets of solutions to Allen-Cahn equation, classification of finite Morse index solutions of Allen-Cahn equation.
On some modified quasilinear Schrödinger equation
杨敏波
浙江师范大学
The aim of this talk is to introduce some existence results for some modified quasilinear Schrödinger equation with different potential and parameter. By using variational methods, we are able to prove the existence of solutions for the quasilinear Schrödinger equation. For different types of quasilinear Schrödinger equation, the deformation arguments and local linking theorem with Morse theory are applied to obtain the existence results.
Solutions concentrating on spheres for coupled Schrödinger systems in dimension four
张建军
重庆交通大学
In this talk, we are concerned with positive vector solutions of Bose-Einstein type systems in dimension four. The interaction is critical in the sense of Sobolev. Via a reduction approach, concentration phenomena around spheres are investigated in the attractive case as the Planck constant goes to zero. This talk is based on joint work with Joao Marcos do O.
Existence and blow-up of ground state solutions for some Kirchhoff equations
张贻民
武汉理工大学
For some Kirchhoff functionals, we search for its L^2-normalized critical points. Firstly, we give a complete classification with respect to the exponent p for the existence of minimizers of these functionals, and show that the minimizer of these functionals, if exists, is unique up to translations. Secondly, we search for the mountain pass type critical point for these functionals on L^2 constraint manifold, and also prove that this type critical point is unique up to translations. Moreover, we get some blow up properties ground state solutions for this type Kirchhoff equations.




 当前位置:
当前位置: